简单介绍
LSTM 是一类循环神经网络,它的提出是为了化解传统循环神经网络(RNN)在 back propagation 中梯度弥散问题,这导致了 RNN 的短期记忆问题,使得 RNN 不能学习长距离的依赖关系。LSTM 通过引入 \(sigmoid\) 控制门来控制信息的保留和丢弃,使得它能够记住重要的信息,遗忘不重要的信息
LSTM 几个重要的门介绍
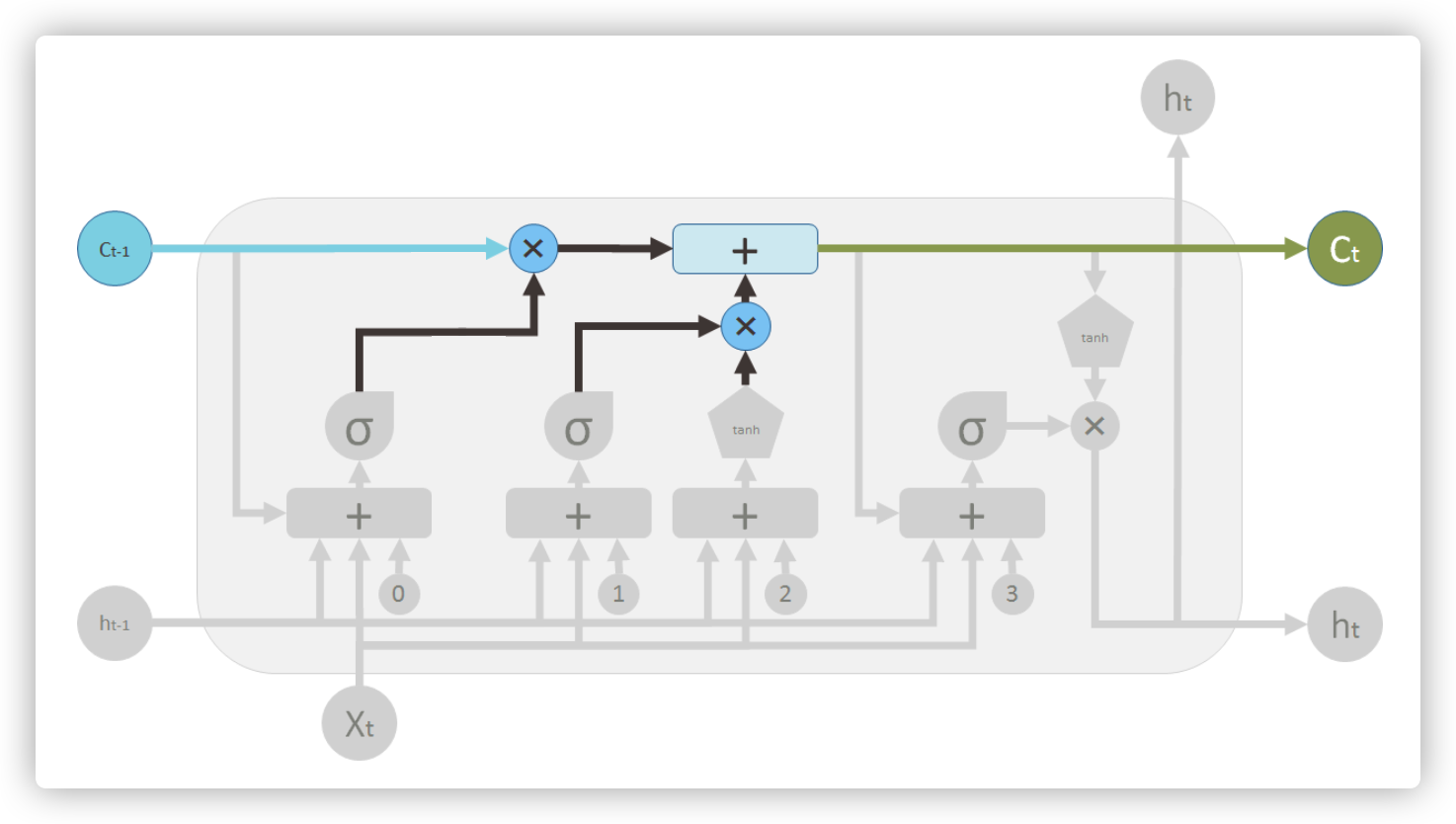
从 Understanding LSTM and its diagrams 这个博客中,我找到了一个最佳的描述 LSTM 细节的图。这是 LSTM 的一个胞元结构,它有两条主要的水平方向的数据流,上面的是胞元状态(\(C_{t-1}\) 包含了 \(t-1\) 时刻及以前序列的信息),下面的是输出或者隐状态(\(h_t\) 包含了当前输入 \(x_t\) 的重要信息)。下面我们介绍下 LSTM 的三个控制门 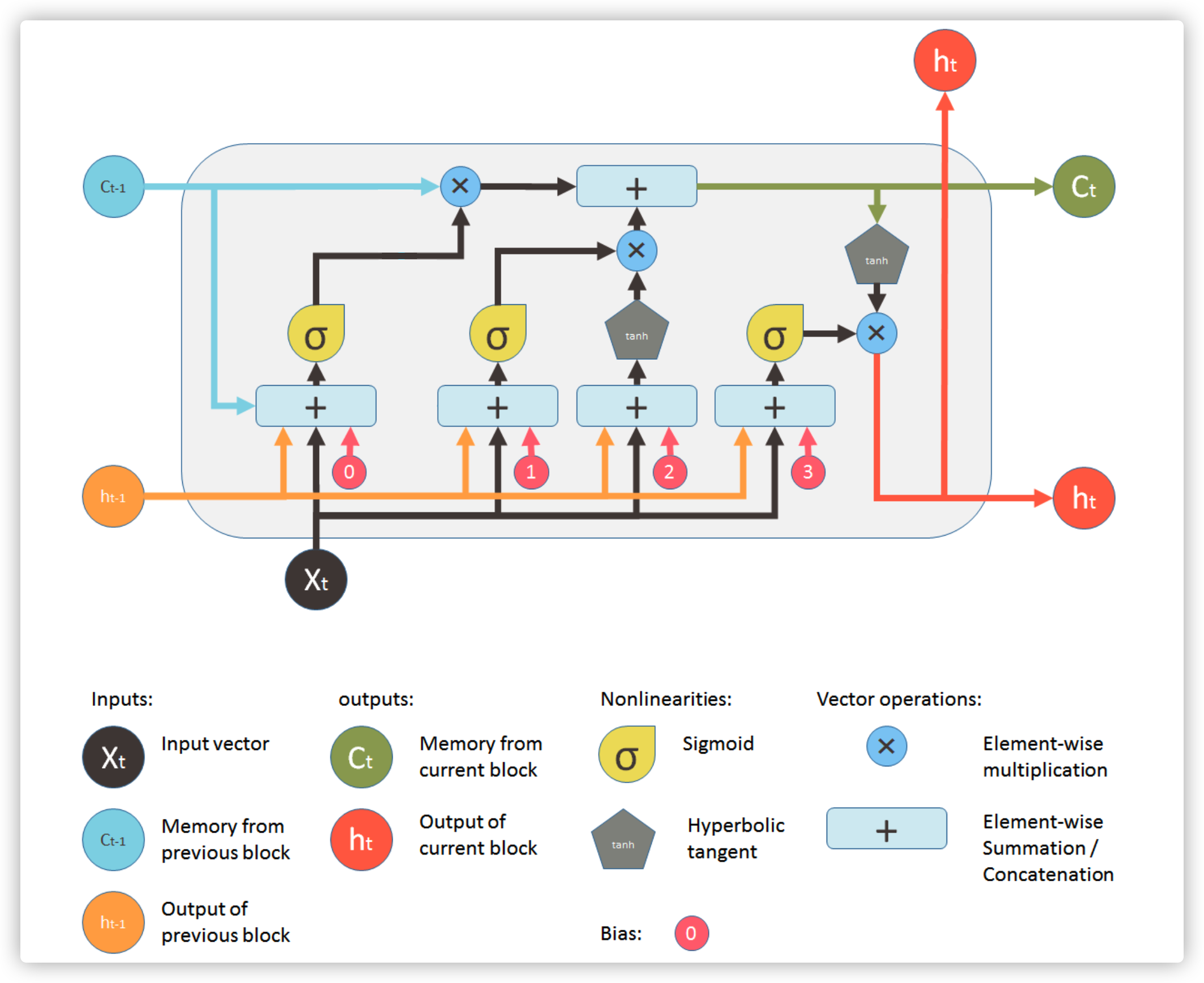
遗忘门
遗忘门根据隐状态 \(h_t\) 和当前输入 \(x_t\) 来决定遗忘 \(C_{t-1}\) 中的哪些信息,其中 \(\sigma(x)=\frac{1}{1+e^{-x}}\) 是一个将输入向量的每一位映射到 \((0,1)\) 的函数,映射后的值越大,\(C_{t-1}\) 的信息保留越多,反之则遗忘越多
\(f_t=\sigma(W_f \cdot [h_{t-1}, x_t] + b_f)\) 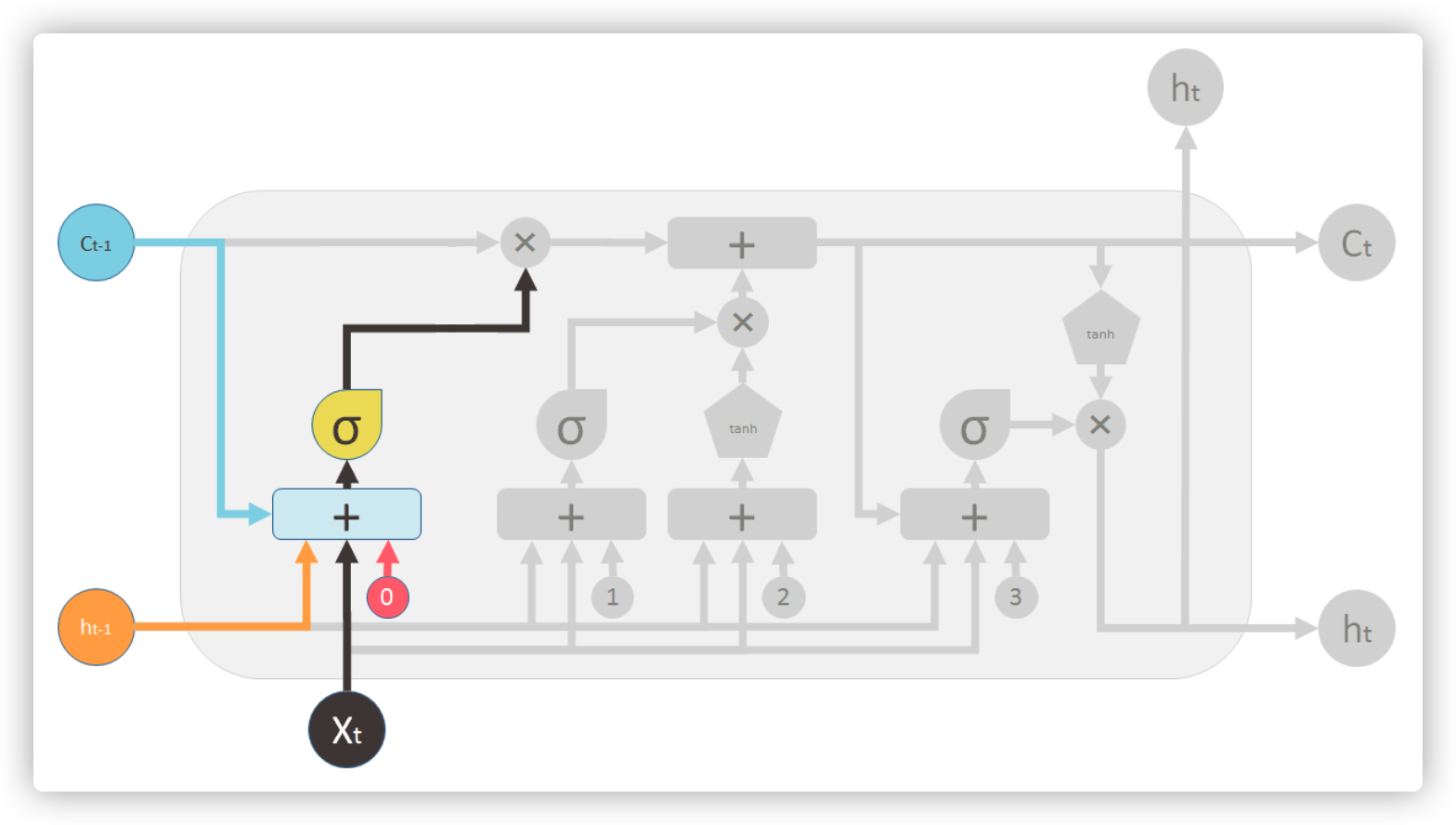
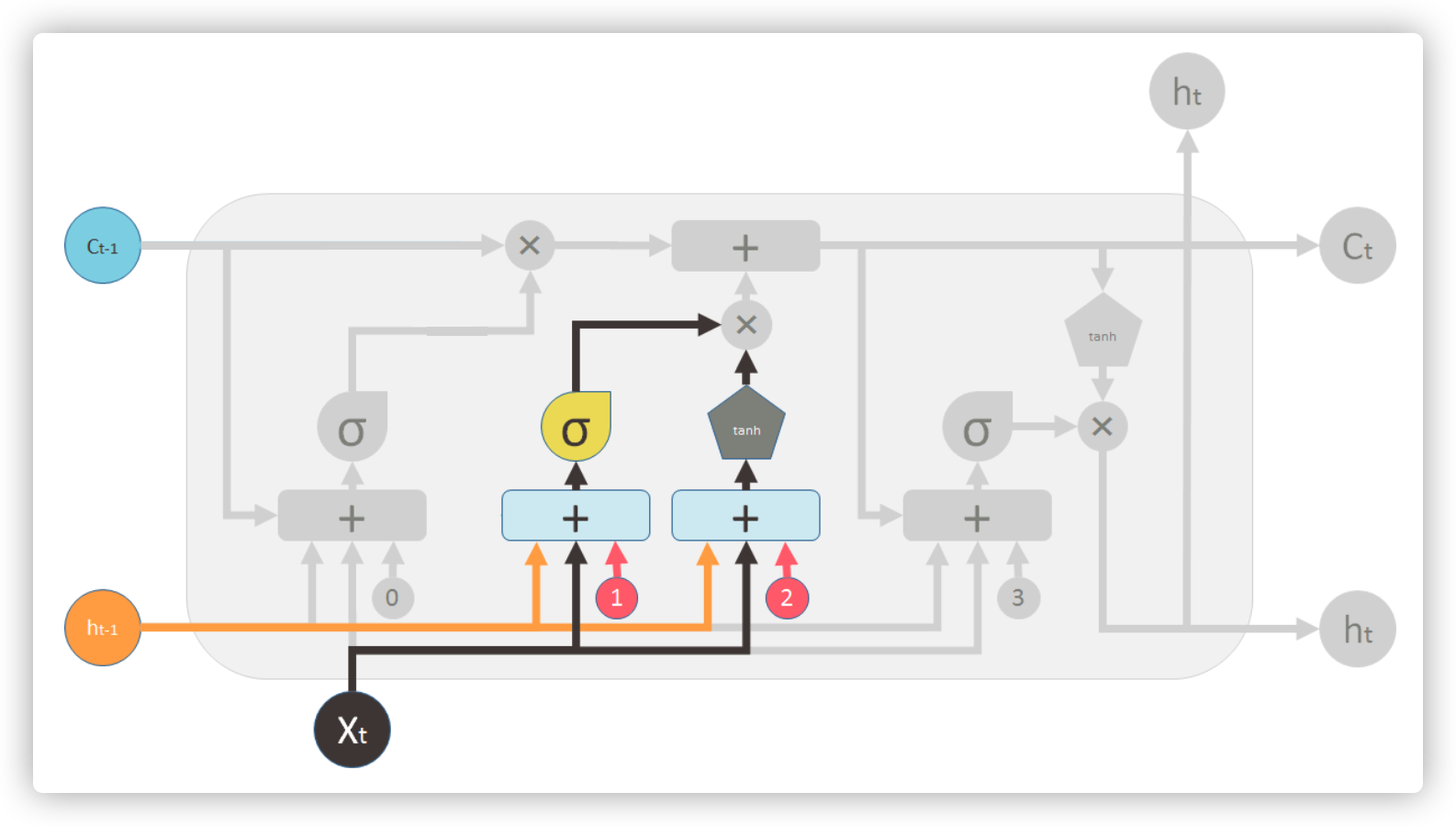
输入门
输入门根据输入 \(x_t\),前一时刻输出 \(h_{t-1}\) 和前一时刻胞元状态 \(C_{t-1}\) 来计算 \(t\) 时刻下的胞元状态 \(C_t\),其中 \(f_t\otimes C_{t-1}\) 是 \(t-1\) 时刻遗忘过后剩余的胞元信息,\(i_t \otimes \tilde{C_{t}}\) 是 \(t\) 时刻新增的胞元状态信息
\(i_t=\sigma(W_i\cdot [h_{t-1}, x_t] + b_i)\)
\(\tilde{C_t}=tanh(W_c\cdot [h_{t-1}, x_t] + b_C)\)
\(C_t=f_t\otimes C_{t-1}+i_t \otimes \tilde{C_t}\)
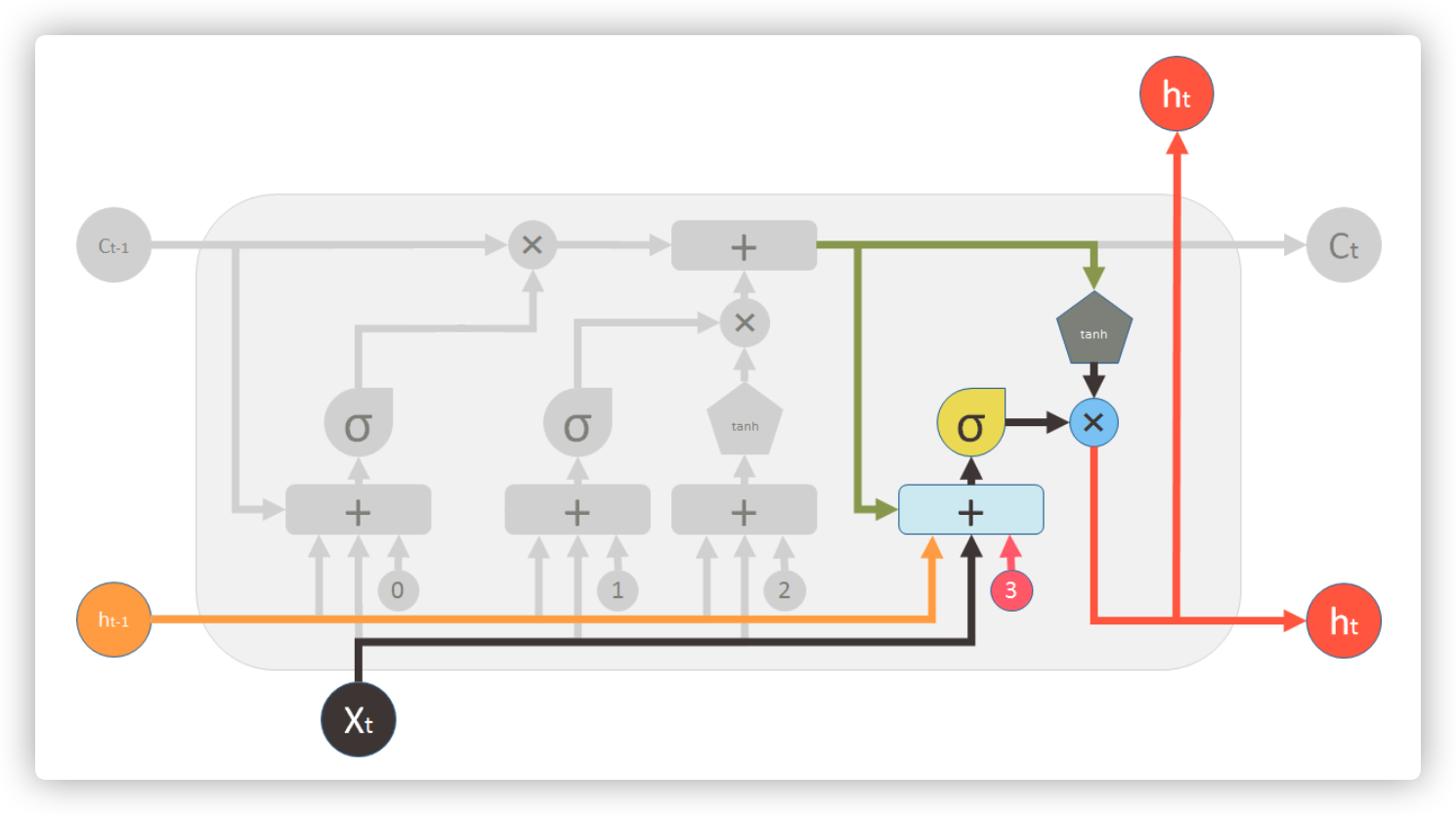
输出门
输出门根据 \(t-1\) 时刻的输出,\(t\) 时刻的输入 \(x_t\) 和 \(t\) 时刻的胞元信息来计算 \(t\) 时刻的输出信息
\(o_t=\sigma(W_o\cdot [h_{t-1}, x_t] + b_o)\)
\(h_t=o_t\otimes tanh(C_t)\)